값 형식 : 변수가 값을 담는 데이터 형식
참조 형식 : 변수가 값 대신 값이 있는 곳의 위치를 담는 데이터 형식
스택, 힙 영역
값 형식
데이터를 쌓는 형식
코드 블록 안에서 생성된 모든 값 형식의 변수들은 "}"를 만나면 제거된다.
참조 형식
힙(데이터) -> 스택(주소)
스택 영역에 저장되어 있는 주소는 코드 블록이 끝나는 시점에 제거되지만
힙 영역에 저장되어 있는 데이터는 더 이상 참조하는 곳이 없을 때 가비지 콜렉터가 수거해 간다.
값 형식 : 변수가 값을 담는 데이터 형식
참조 형식 : 변수가 값 대신 값이 있는 곳의 위치를 담는 데이터 형식
스택, 힙 영역
값 형식
데이터를 쌓는 형식
코드 블록 안에서 생성된 모든 값 형식의 변수들은 "}"를 만나면 제거된다.
참조 형식
힙(데이터) -> 스택(주소)
스택 영역에 저장되어 있는 주소는 코드 블록이 끝나는 시점에 제거되지만
힙 영역에 저장되어 있는 데이터는 더 이상 참조하는 곳이 없을 때 가비지 콜렉터가 수거해 간다.
우선, Sigmoid 함수의 문제점을 말하기 위해 기존의 NN이 어떤식으로 동작하는지 복습해보자.

Input 데이터가 NN을 거쳐서 Output이 도출되고 그 Output과 실제 데이터의 차이를 loss(cost)라고 하며 이 loss의 미분을 통하여 Backpropagation 하여 NN을 학습시킨다.
그렇다면 loss의 미분은 기울기라고 할 수 있는데 sigmoid 함수의 특징상 양쪽으로 갈수록 기울기가 0에 가까워지며 그런 값들이 계속해서 곱해지면 결국 gradient가 소실되는 상황이 발생하고 Backpropagation 단계에서 이전 층이 전달받을 gradient가 없게 되는 현상이 생기는데 그것을 Vanishing Gradient라고 하고 이 현상이 sigmoid 함수의 문제점이라 할 수 있다. ( 양 극단의 미분값이 0이 되는 문제 )
위와 같은 문제를 해결할 수 있는 방법중 하나는 Relu 함수를 쓰는 것이다.
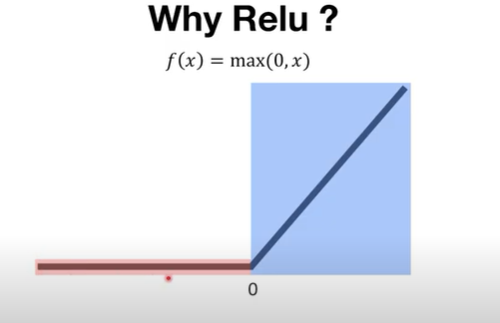
Relu 함수는 위와 같은 형태를 띠는데 0 이상일때 y=x 즉, gradient가 1이 되므로 네트워크의 층이 많아도 문제가 발생하지 않는다. 다만, 0 이하일때 즉, 음수일때는 기울기가 0이 되므로 문제가 발생한다. 그럼에도 효율적이고 간단해서 많이 사용된다.
| 12. Neural Nets(NN) for XOR (0) | 2020.04.28 |
|---|---|
| 11. Deep Neural Nets (0) | 2020.04.28 |
| 10. Training/Testing data set (0) | 2020.04.24 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |
이번에는 Neural Network를 통해 학습에 문제였던 XOR 문제를 어떻게 푸는지 확인해보자.
초기의 단층의 시스템으로는 XOR 문제를 풀 수 없다는 것이 수학적으로 증명이 되었고 이후 여러층을 가진 시스템을 구성하면서 해결책을 제시했고 그 과정에서 각 층의 W, b를 구하는 것이 다시 문제가 되었다.
그렇다면 3개의 Logistic Regression을 통해(Neural Net) 어떤 식으로 XOR 문제를 해결하였는지 확인해보자.

위의 그림은 XOR 문제를 해결하는 하나의 예시이다. 위와 같이 하나의 시스템이 아닌 여러개의 시스템을 이용하여 우리가 원하는 XOR 문제의 결과를 도출해낼 수 있다.
x1 = 0, x2 =0 일때, XOR을 수행하면 0이 나와야 하는데 그 과정을 예로 들어 보겠다.
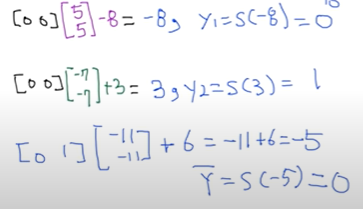

sigmoid 함수를 사용하면 위와 같은 결과가 나올 것이다. 여기서 y1, y2를 구하는 시스템에서 sigmoid 함수를 사용하지 않아도 결과는 같게 나온다.
위의 결과는 임의의 W, b 값을 주어준 상태로 결과 값을 도출해낸 것으로 XOR의 계산이 가능하다는 것을 보여준다.
결과적으로 아래와 같은 형태를 띨 것이다.

또한 x 데이터를 받는 두 개의 Logistic Regression은 아래와 같이 Vector 단위로 하나로 묶일 수 있다.

그렇다면 TensorFlow를 활용한 코드로 NN을 이해해보자.
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
# 랜덤시드
tf.compat.v1.set_random_seed(777)
# 데이터 셋
x_data = [[0, 0],
[0, 1],
[1, 0],
[1, 1]]
y_data = [[0],
[1],
[1],
[0]]
# 데이터 셋 구성
dataset = tf.data.Dataset.from_tensor_slices((x_data, y_data)).batch(len(x_data))
# 데이터 전처리
def preprocess_data(features, labels):
features = tf.cast(features, tf.float32)
labels = tf.cast(labels, tf.float32)
return features, labels
# weight, bias 선언 3개의 시스템
W1 = tf.Variable(tf.random.normal([2, 1]), name="weight1")
b1 = tf.Variable(tf.random.normal([1]), name="bias1")
W2 = tf.Variable(tf.random.normal([2, 1]), name="weight2")
b2 = tf.Variable(tf.random.normal([1]), name="bias2")
W3 = tf.Variable(tf.random.normal([2, 1]), name="weight3")
b3 = tf.Variable(tf.random.normal([1]), name="bias3")
# NN 구현 layer1, layer2 -> layer3
def neural_net(features):
layer1 = tf.sigmoid(tf.matmul(features, W1) + b1)
layer2 = tf.sigmoid(tf.matmul(features, W2) + b2)
# tf.concat 함수를 통해 데이터 횡방향 연결
layer3 = tf.concat([layer1, layer2], -1)
layer3 = tf.reshape(layer3, shape=[-1, 2])
hypothesis = tf.sigmoid(tf.matmul(layer3, W3) + b3)
return hypothesis
# cost 함수 구현
def loss_fn(hypothesis, labels):
cost = -tf.reduce_mean(labels * tf.math.log(hypothesis) + (1 - labels) * tf.math.log(1 - hypothesis))
return cost
# 정확도 측정 함수 구현
def accuracy_fn(hypothesis, labels):
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, labels), dtype=tf.float32))
return accuracy
# 학습 (cost minimize)
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
def grad(hypothesis, features, labels):
with tf.GradientTape() as tape:
loss_value = loss_fn(neural_net(features), labels)
return tape.gradient(loss_value, [W1, W2, W3, b1, b2, b3])
EPOCHS = 5000
for step in range(EPOCHS):
for features, labels in iter(dataset):
features, labels = preprocess_data(features, labels)
grads = grad(neural_net(features), features, labels)
optimizer.apply_gradients(grads_and_vars=zip(grads, [W1, W2, W3, b1, b2, b3]))
if step % 500 == 0:
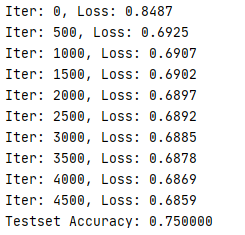
print("Iter: {}, Loss: {:.4f}".format(step, loss_fn(neural_net(features), labels)))
x_data, y_data = preprocess_data(x_data, y_data)
test_acc = accuracy_fn(neural_net(x_data), y_data)
print("Testset Accuracy: {:4f}".format(test_acc))
결과
| 13. Relu (0) | 2020.04.30 |
|---|---|
| 11. Deep Neural Nets (0) | 2020.04.28 |
| 10. Training/Testing data set (0) | 2020.04.24 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |
초기의 인공지능은 XOR 문제를 풀 방법이 없어서 불가능하다고 생각되었다.

그렇게 시간이 지나고 Paul Werbos이라는 분에 의해서 에러를 결과에서 도출해서 반대로 W, b를 구하는 방식의 Backpropagation이라는 알고리즘이 해결책으로 제시되었다.

또한, 그것을 토대로 Convolutional Neural Networks라는 것이 개발되었다.

그러나 Backpropagation 알고리즘이 많은 층이 있을 때 학습을 제대로 시키지 못하는 문제가 발생한다.
이후에 그런 문제를 해결하기 위해 연구를 진행하다가 각각의 weight 값을 초기값을 주는 과정에서 초기값을 잘 주어주면 문제가 해결되어 학습이 된다는 것을 확인하였고 Deep Learning이라는 명칭이 생겼다.
이미지를 판별해내는 IMAGENET 챌린지 등을 통해 인공지능에 대한 관심이 커졌고 그 이후에는 많은 발전을 통해 자연어 처리, 게임 인공지능, 알파고 등 많은 인공지능이 개발된다.
현재에는 TensorFlow와 같은 쉬운 툴, Python과 같은 언어가 발전함에 따라 Deep Learning을 공부하기 좋은 환경을 갖추고 있다.
| 13. Relu (0) | 2020.04.30 |
|---|---|
| 12. Neural Nets(NN) for XOR (0) | 2020.04.28 |
| 10. Training/Testing data set (0) | 2020.04.24 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |
우리가 만든 머신러닝 모델이 얼마나 잘 작동하는지 확인하는 방법에 대해 알아보겠다.
일정한 학습 데이터 셋(Training data set)를 이용하여 모델을 만들고 같은 데이터 셋으로 모델을 테스트하면 당연하게 올바른 결과가 나올 것이다. 그러나 같은 데이터 셋을 사용하여 테스트하는 것은 실질적으로 의미가 없다. 다른 데이터가 들어올 때 올바르게 반응해야 그것이 제대로 된 모델이라고 할 수 있다.
그렇게 학습 때와는 다른 데이터로 모델을 테스트하기 위해 우리는 데이터 셋에서 Training을 위한 데이터와 Test를 위한 데이터를 나눌 필요가 있다.

위의 사진과 같이 우리가 가지고 있는 데이터 셋에서 학습을 위한 데이터와 테스트를 위한 데이터를 나누고 실제 모델을 만들 때는 학습 데이터 셋만을 사용하여 모델을 생성하고 생성된 모델을 가지고 테스트 데이터 셋을 사용하여 모델이 잘 만들어졌는지 테스트해본다. ( 보통 Training data와 Test data는 7:3의 비율 정도로 나눈다고 함 )

위와 같이 Traing data와 Testing data를 나눌 수 있는데 특별히 우리가 필요한 알파나 람다와 같은 상수를 정해주기 위해 training data를 Training data와 Validation data로 나누기도 한다. ( Validation data를 이용하는 것은 시험을 치기 위해 모의고사를 보는 것과 비슷한 의미 )
Online learning
데이터 셋이 많을 때 메모리와 같은 부분이 부족할 수 있기 때문에 이 데이터를 나누어서 학습을 시켜주는 것을 Online learning이라고 한다. ( 학습 데이터가 추가될 경우에 사용하는 방식이기도 하다. )
Mnist Dataset

위와 같이 숫자를 구별하는 모델을 위한 유명한 데이터 셋인 Mnist Dataset도 마찬가지로 Training을 위한 데이터( images, labels )와 Testing을 위한 데이터( images, labels )가 나누어져 있는 것을 볼 수 있다.
결과적으로 Training dataset을 이용하여 학습한 모델을 만들고 Testing dataset으로 Accuracy(정확도)를 알아내어 높은 정확도의 모델을 만드는 것이 최종 목적이다.
그렇다면 실습을 통해 소스코드를 구현해보자.
import tensorflow as tf
x_data = [[1, 2, 1],
[1, 3, 2],
[1, 3, 4],
[1, 5, 5],
[1, 7, 5],
[1, 2, 5],
[1, 6, 6],
[1, 7, 7]]
y_data = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[1, 0, 0],
[1, 0, 0]]
# Evaluation our model using this test dataset
x_test = [[2, 1, 1],
[3, 1, 2],
[3, 3, 4]]
y_test = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1]]
X = tf.placeholder("float", [None, 3])
Y = tf.placeholder("float", [None, 3])
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))
# 가설 및 entropy 함수를 통한 cost function 구현
hypothesis = tf.nn.softmax(tf.matmul(X, W)+b)
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# ONE-HOT encoding을 통해 변환한 예측값, 실제값을 비교하여 정확도 측정
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# 학습 데이터를 통한 학습 과정
for step in range(201):
cost_val, W_val, _ = sess.run([cost, W, optimizer],
feed_dict={X: x_data, Y: y_data})
print(step, cost_val, "\n", W_val)
# predict
print("Prediction: ", sess.run(prediction, feed_dict={X: x_test}))
# Calculate the accuracy
print("Accuracy: ", sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))
우선 학습을 위한 x_data, y_data 그리고 테스트를 위한 x_test, y_test로 데이터를 나눈다.
이전과 같은 방식으로 학습 데이터를 통해 모델을 만들고 테스트 데이터를 통해 모델을 평가한다.
결과

결과적으로 학습 데이터를 통해 만든 모델이 우리가 설정한 테스트 데이터에서도 100%의 확률로 예측에 성공하였다는 것을 볼 수 있다. 이로써 training dataset과 testing dataset을 나누어 우리의 모델을 평가하는 부분까지 끝났다.
이제는 이런 평가를 통해 이전에 공부했던 Learning rate 적정값 설정의 필요성과 Normalization의 필요성을 소스코드를 통해 이해해보자.
앞선 코드에서는 learning_rate를 0.1로 주었는데 이번에는 1.5와 1e-20으로 각각 주어주고 결과값을 확인해보자.
결과 (learning_rate=1.5)

결과 (learning_rate=1e-20)

learning_rate를 크게 설정하니 cost 값이 nan이 되고 결과적으로 정확도가 0이 되는 것을 확인할 수 있다.
또한, learning_rate를 작게 설정하니 cost 값이 일정 횟수 이상이 될때 같은 결과로 나오며 이 또한 정확도가 0이 되는 것을 확인할 수 있다.
learning rate을 잘 설정했음에도 불구하고 nan이 나오는 경우가 있는데 많은 이유 중 하나가 input 데이터가 Normalized 되지 않았기 때문이다. Normalization의 한 예로 아래와 같이 MinMaxScaler이라는 함수를 사용하여 0~1 사이의 값으로 변경시켜주고 그 데이터를 input 데이터로 사용한다.

Non-normalized input을 이용한 소스코드
import tensorflow as tf
import numpy as np
xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
[823.02002, 828.070007, 1828100, 821.655029, 828.070007],
[819.929993, 824.400024, 1438100, 818.97998, 824.159973],
[816, 820.958984, 1008100, 815.48999, 819.23999],
[819.359985, 823, 1188100, 818.469971, 818.97998],
[819, 823, 1198100, 816, 820.450012],
[811.700012, 815.25, 1098100, 809.780029, 813.669983],
[809.51001, 816.659973, 1398100, 804.539978, 809.559998]])
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
cost_val, hy_val, _ = sess.run([cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)
결과

Normalized input을 이용한 소스코드
import tensorflow as tf
import numpy as np
def min_max_scaler(data):
numerator = data - np.min(data, 0)
denominator = np.max(data, 0) - np.min(data, 0)
# noise term prevents the zero division
return numerator / (denominator + 1e-7)
xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
[823.02002, 828.070007, 1828100, 821.655029, 828.070007],
[819.929993, 824.400024, 1438100, 818.97998, 824.159973],
[816, 820.958984, 1008100, 815.48999, 819.23999],
[819.359985, 823, 1188100, 818.469971, 818.97998],
[819, 823, 1198100, 816, 820.450012],
[811.700012, 815.25, 1098100, 809.780029, 813.669983],
[809.51001, 816.659973, 1398100, 804.539978, 809.559998]])
xy = min_max_scaler(xy)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
cost_val, hy_val, _ = sess.run([cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)
결과

| 12. Neural Nets(NN) for XOR (0) | 2020.04.28 |
|---|---|
| 11. Deep Neural Nets (0) | 2020.04.28 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |
| 7. Logistic Regression (0) | 2020.04.20 |
TensorFlow를 활용한 실습 코드에서 Gradient descent 알고리즘을 사용할 때 항상 Learning rate을 주었는데 이때, Learning rate이라는 것은 한 Step의 크기라고 할 수 있다.
Learning rate이 클 때 우리가 원하는 cost function의 minimize를 아래와 같이 수행하지 못하는 현상이 일어날 수 있는데 그것을 overshooting이라고 한다. ( 그래프를 벗어나거나 원하는 목적지에 도달하지 못함 )
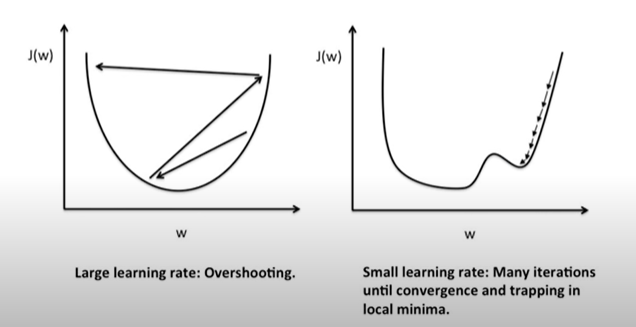
반대로 Learning rate이 작으면 시간이 너무 오래 걸리거나 정확한 목적지에 도달하기도 전에 minimum을 잡아 버리는 경우가 발생하므로 이 Learning rate을 너무 크지도 너무 작지도 않은 적정값으로 설정하는 것이 중요하다.
( 우리의 데이터나 환경에 따라 적절한 Learning rate은 다르지만 보통 0.01로 잡고 시작한다. )
우리가 학습을 진행하다 보면 데이터 (특히, X 데이터)를 선처리 해야하는 경우가 있다.
데이터 간에 큰 차이가 있을 경우에 적절한 Learning rate을 잡아도 학습이 아래와 같이 제대로 이루어지지 않을 경우가 생긴다.
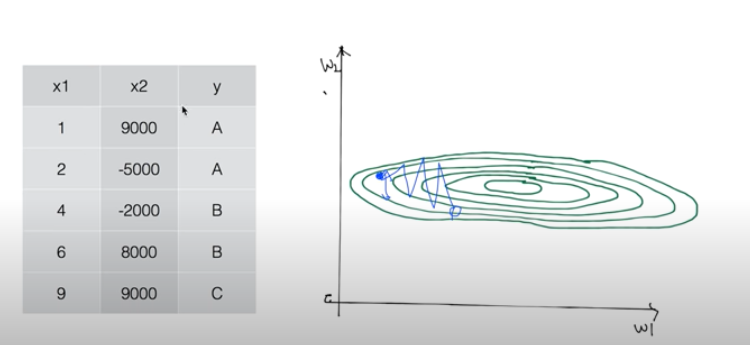
이런 현상을 해결하기 위해 우리는 데이터를 아래와 같이 Normalize 할 필요가 있다.
(원본 데이터의 중심을 0으로 만들고 데이터가 일정 범위 내의 값이 될 수 있도록 변경시켜준다.)
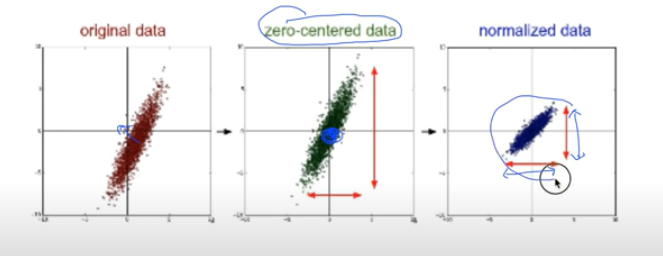
Standardization
Normalization 방식은 여러가지가 있고 필요에 맞게 X 데이터를 처리하는 것이 우리의 학습이 좋은 성능을 발휘하기 위한 좋은 방법이다. 아래는 Normalization 방식 중 Standardization을 구현하는 방법이다.

우리의 모델이 우리가 학습한 데이터에 너무 맞게 생성될 경우 우리의 학습 데이터에만 올바르게 작동하고 새로운 데이터에는 올바르게 작동하지 않을 경우가 생기는데 이런 현상을 overfitting이라고 한다.

위의 두번째 경우에서 우리가 학습시킨 데이터에만 치중된 모델이 생성되므로 새로운 데이터가 들어올 경우 이 모델이 제대로 작동하지 않을 수가 있다.
Overfitting을 해결하기 위한 방법은 여러 가지가 존재하는데,
1. 학습 데이터의 종류를 늘린다.
2. X 데이터의 개수(features)를 줄인다.
3. Regularization (일반화)
Regularization
weight의 편차가 너무 크거나 개수가 많아지면 두번째 모델과 같은 형식을 띨 수 있는데, 이렇게 구부러진 형태의 모델을 첫 번째 모델과 같이 펼칠 수 있도록 해 주는 것이 Regularization이라 한다.

Cost function의 뒤에 위와 같은 항을 추가 시켜서 구현할 수 있다. 위의 항은 weight의 제곱을 전부 더해준 값에 regularization strength라고 하는 상수를 곱해주면 되는데 이때, 상수가 하는 역할은 regularization의 중요도를 의미하며 상수가 0이 되면 정규화를 하지 않는다는 말이고 1이면 중요하게 생각한다는 의미이다.(상수에 따라 해당 항의 크기가 달라지니..)
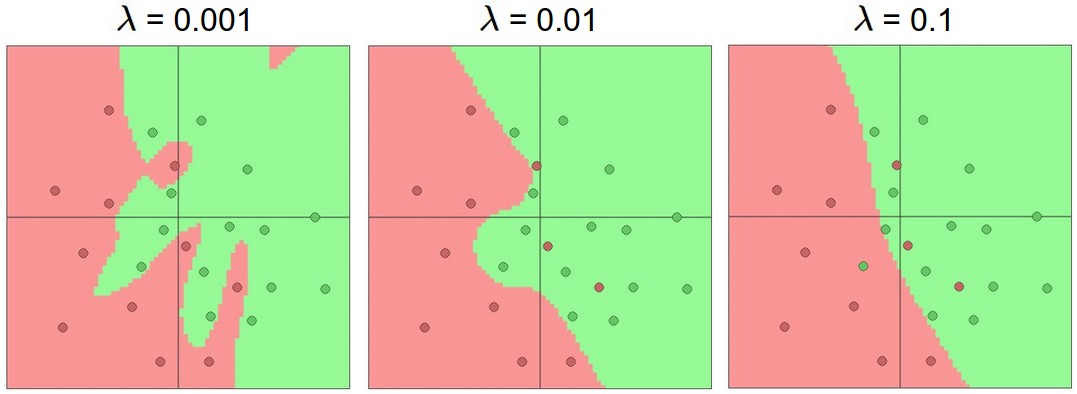
| 11. Deep Neural Nets (0) | 2020.04.28 |
|---|---|
| 10. Training/Testing data set (0) | 2020.04.24 |
| 8. Softmax classification (0) | 2020.04.22 |
| 7. Logistic Regression (0) | 2020.04.20 |
| 6. Loading Data from File (0) | 2020.04.18 |
# softmax 부분의 강의는 tensorflow 1.x 버전을 기준으로 작성하였습니다.
이제는 Pass와 Fail의 두 가지 output을 가지는 것이 아니라 3가지 이상의 output을 가진 Multinomial classification에 대하여 알아볼 것이다.
그렇다면 공부시간, 출석을 가지고 성적을 예측하는 Multinomial Classification을 가지고 이해해보자.

위의 A, B, C라는 output을 가지는 y를 Binomial classification의 방식을 이용하여 나누는 작업을 해보자.
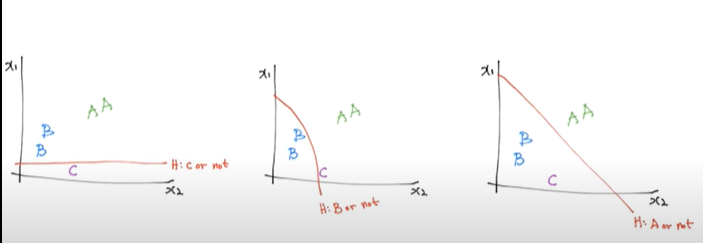

(C or Not), (B or Not), (A or Not)의 세 가지 Binomial classification 방식을 사용하여 Multinomial classification을 구현하였다.
오른쪽 사진은 Binomial 방식을 그림으로 표현한 것인데 설명하자면 input인 X 값이 weight(가중치)를 거쳐서 z가 되고 이 z가 sigmoid 함수를 거쳐서 Y-hat이 된다. Y-hat의 의미는 실제 output이 될 수 있는 1과 0인 Y에 반해 sigmoid를 거친 z의 값은 0~1 사이의 값을 가질 수 있고 그 값을 Y-hat이라고 표현한다.
결과적으로 이 Multinomial classification을 Matrix로 표현하면 아래와 같은 형태가 될 것이다.

그런데 이렇게 독립적으로 Matrix를 계산하는 것보다 하나의 Matrix로 합쳐서 계산하는 것이 효율적이기 때문에 Matrix를 합쳐주는 과정을 수행하여 준다.

이전의 방식은 Matrix의 곱을 수행하면 하나의 Scalar 값으로 반환되는데 합친 Matrix의 곱은 Vector 형식으로 반환됨을 볼 수 있다.
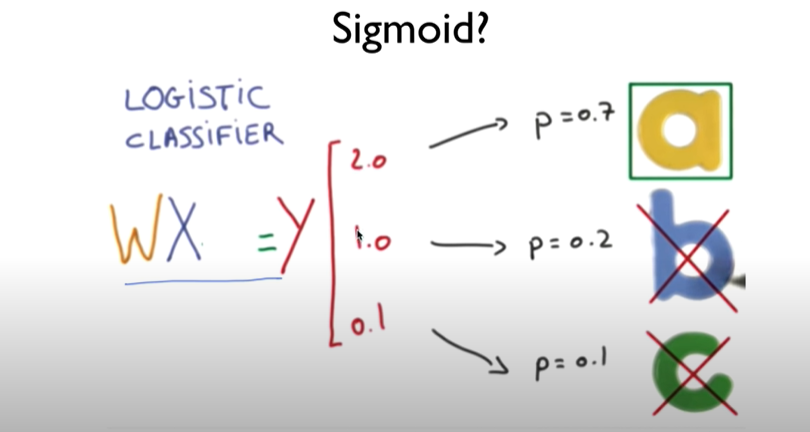
Binomial classification에서는 행렬 곱에 의해 반환된 값을 sigmoid 함수를 이용하여 0~1 사이의 값으로 변환시켜주었지만 Multinomial classification에서는 softmax 함수를 이용하여 0~1 사이로 변환시켜주며 합이 1이 되게 만든다.
(합이 1이라는 의미는 각각의 값이 확률이 된다는 의미이다. 위의 이미지에서 a는 0.7, b는 0.2, c는 0.1의 확률을 가지게 된다.)
그럼 우리의 output은 우리가 구한 확률이 아니라 특정 값이 되며 위의 예에서는 A or B or C가 되므로 이 확률을 가지고 A인지 B인지 C인지 구분해내는 과정이 필요한 것이다.

A, B, C를 구분해내기 위한 과정 중 확률이 가장 높은 것을 1로 만들어 주고 나머지를 0으로 만들어 주는 알고리즘을 ONE-HOT encoding이라고 하며 이 알고리즘을 통해 반환되는 1 또는 0을 통해 A, B, C를 결정지어준다.
(TensorFlow에서는 argmax라는 함수를 이용하여 이 알고리즘을 구현한다.)
그렇다면 이제 우리가 구한 S(y) 값과 실제 label인 Y 값을 통하여 cost function을 구하고 Minimize 하는 과정을 거쳐서 우리가 원하는 weight 값을 구하고 모델을 만들어야 한다. (우리가 예측한 값이 맞는지 틀린지에 대한


S(y)와 L 값(Y 값)의 차이를 구하기 위하여 CROSS-ENTOROPY라는 함수를 사용한다.
CROSS-ENTOROPY 함수를 사용하는 이유는 위의 이미지와 같이 우리가 예측한 S(y) 값과 실제 데이터 레이블인 L 값이 일치할 때는 0 일치하지 않을 때는 무한대로 결과가 나오기 때문에 일치할 때는 작은 값, 일치하지 않을 때는 큰 값이 나오는 cost function의 특성을 만족하기 때문이다.
S(y)와 cost function을 이용하여 측정하고자 하는 것은 맞추냐 못 맞추냐가 아니라 확률적으로 얼마나 정확히 맞추냐이므로 S(y) 값을 활용해야 하고(ONE-HOT encoding을 통해 반환되는 값이 아닌)
만약 0.7, 0.2, 0.1으로 예측한 위의 알고리즘과 0.8, 0.1, 0.1으로 예측한 새로운 알고리즘이 있다면 후자가 더 우월한 알고리즘이라는 것을 이러한 cost function으로 알아낼 수 있다.
결과적으로 아래와 같은 cost function을 결정할 수 있다.

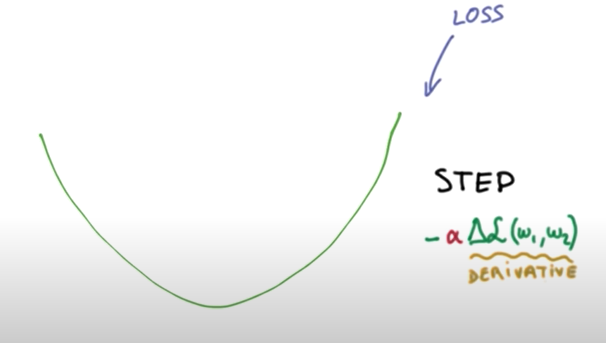
마지막으로 cost function을 minimize 해주어야 하는 W vector을 찾아주는 gradient descent 알고리즘을 사용하면 될 것이다. ( cost function의 미분을 통해 W 값을 update 하는 방식 )
이제 실제로 TensorFlow를 이용하여 실습해보자.
TensorFlow에서는 softmax 함수를 제공하기 때문에 식으로 표현할 필요 없이 함수를 가져다 쓰면 된다.
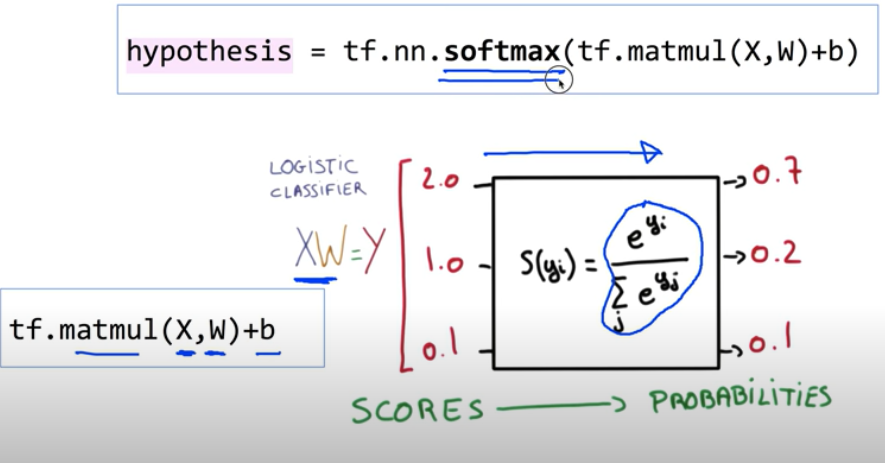
softmax 과정을 거친 hypothesis을 가지고 cost function을 구현하고 minimize까지 완료하면 전체적인 모델 구성이 완료된다. (cross entropy 함수 형식을 사용)

코드
import tensorflow as tf
# x 데이터와 y 데이터 셋
x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5],
[1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]
# x 데이터셋의 크기는 n*4
# y 데이터셋의 크기는 n*3
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
# W의 크기는 [X data Column, Y data Column]
# b의 크기는 [Y data Column]
# 여기서 X는 입력 데이터 Y는 출력 데이터
# Variable은 TensorFlow가 자체적으로 변경시키는 것 (trainable)
# 랜덤한 값으로 주어 줌
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax를 이용하여 softmax 함수 사용
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy를 사용한 cost function 구현
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
a = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9],
[1, 3, 4, 3],
[1, 1, 0, 1]]})
print(a, sess.run(tf.arg_max(a, 1)))
결과

위의 소스코드를 구현함에 있어 복잡함을 줄이기 위해 TensorFlow에서 제공하는 함수를 이용해 보고 동물의 데이터를 통해 종을 분류하는 프로그램을 짜 보자.
import tensorflow as tf
import numpy as np
# Numpy의 loadtxt 함수를 이용하여 csv 파일 읽기
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
# x의 데이터 셋은 읽어온 파일의 전체행, 마지막 열(y) 데이터 제외
x_data = xy[:, 0:-1]
# y의 데이터 셋은 읽어온 파일의 전체행, 마지막 열(y)만
y_data = xy[:, [-1]]
# 클래스 개수 ( y가 0 ~ 6의 값을 가지므로 )
nb_classes = 7
# X, Y를 placeholder로 만들어 실행 단계에서 값을 넣어 줄 수 있도록 구현
# x(input)의 개수는 16, y(output)의 개수는 1 (0~6의 클래스 개수를 가진 1개의 y)
X = tf.placeholder(tf.float32, [None, 16])
Y = tf.placeholder(tf.int32, [None, 1])
# Y는 one-hot이 아닌 데이터이기 때문에 one-hot으로 바꿔주어야 한다.
Y_one_hot = tf.one_hot(Y, nb_classes)
# one_hot 함수를 이용하면 차원이 1차원 더해지기 때문에 reshape 함수를 통해 차원을 다시 맞춰주어야한다.
# [None, 7] 형태로 변환
Y_one_hot = tf.reshape(Y_one_hot, [-1, nb_classes])
# W, b 의 값을 변동가능한 Variable로 만들어 주고 16개의 input 종류를 가지고 one-hot을 거친 7개의 output
W = tf.Variable(tf.random_normal([16, nb_classes]), name = 'weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# 우리가 원하는 식을 세우고 softmax 함수를 통해 가설이 만듦
logits = tf.matmul(X, W) + b
hypothesis = tf.nn.softmax(logits)
# Cross entropy를 통한 cost function 구현
# 식을 직접 구현하는 것이 아닌
# softmax_cross_entropy_with_logits 함수를 이용하여 cross entropy 구현
cost_i = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# 예측한 값의 정확도를 확인하기 위해 accuracy 구현
prediction = tf.argmax(hypothesis, 1)
correct_prediction = tf.equal(prediction, tf. argmax(Y_one_hot, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2000):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 100 == 0:
loss, acc = sess.run([cost, accuracy], feed_dict={X: x_data, Y: y_data})
print("Step: {:5}\tLoss: {:.3f}\tAcc: {:.2%}".format(step, loss, acc))
pred = sess.run(prediction, feed_dict={X: x_data})
# flatten()은 y_data를 [[1], [0], ..] -> [1, 0, ..] 형태로 변경
# zip은 각각의 list를 p, y로 던져주기 편하게 하나로 묶음
for p, y in zip(pred, y_data.flatten()):
print("[{}] Prediction: {} True Y: {}".format(p == int(y), p, int(y)))
결과
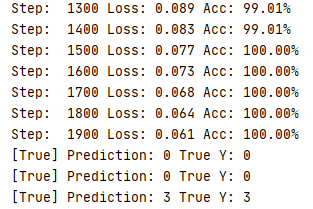
| 10. Training/Testing data set (0) | 2020.04.24 |
|---|---|
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 7. Logistic Regression (0) | 2020.04.20 |
| 6. Loading Data from File (0) | 2020.04.18 |
| 5. Multi-variable linear regression (0) | 2020.04.17 |
Logistic Regression 알고리즘은 정확도가 높은 알고리즘으로 알려져 있어 실제 문제에 적용 가능하며 Nueral Networking과 Deep Learning에 중요한 요소이다.
Regression이란 이름을 가지고 있지만 실제로는 Classification 문제에 사용되는 알고리즘 중 하나이다.
우선 Classification에 대해 Binary Classification의 예를 통해 이해해보자.
1. Spam Email Detection: Spam or Ham
스팸메일을 구분해내는 프로그램은 이메일이 올 때 학습된 모델을 통해 Spam인지 Ham인지 구분한다.
2. Facebook feed: show or hide
페이스북에서는 Classification 알고리즘을 통해 이전에 봤거나 좋아했던 글들을 바탕으로 사용자에게 글들을 맞춤으로 보여준다. (흔히 말하는 유튜브 알고리즘도 마찬가지)
0, 1 encoding
1. Spam Detection: Spam(1) or Ham(0)
2. Facebook feed: show(1) or hide(0)
그렇다면 공부 시간에 따라 합격과 불합격을 예측하는 Classification을 적용해보자.

Pass(1) or Fail(0)이라는 관점에서 데이터를 생각해보면 위와 같이 나올 수 있는데 그렇다면 일부의 데이터를 이용해 직선을 그리고 제일 오른쪽에 있는 데이터가 새로 생겼다는 가정하에 직선을 그려보자.

위의 그래프를 보면 기존에 Pass 취급을 받았던 데이터 2개가 새로 직선을 만들어줌으로써 Fail이 될 수 있는 문제가 발생할 수 있고 이는 Classification의 관점에서 Linear 한 가설은 맞지 않음을 확인할 수 있다.
결론적으로 Linear Regression은 Regression에 맞는 알고리즘, Logistic Regression은 Classification에 맞는 알고리즘이라는 것을 알 수 있다.
또한, 다음 문제점으로 우리가 Pass or Fail과 같이 0과 1 사이의 값으로 이루어지는 Y(결과) 값을 가져야 하는데,
Linear 한 관점에서 우리는 H(x)=Wx+b의 가설을 세우고 W=0.5 b=0으로 가정하면 H(x)=0.5x가 될 것인데, 만약 x=100이라는 데이터가 들어간다면 H(x)는 50이 될 것이며 0, 1과는 거리가 먼 결과 값이 될 것이다. 그렇다면 이런 결과 값을 0과 1 사이의 값으로 변환시켜줄 필요가 있지 않을까? ( 결과적으로 Linear 한 가설은 Classification의 관점에 맞지 않다. )

위의 함수는 데이터를 새로운 함수에 넣고 구현함으로써 0과 1 사이의 값으로 변환시켜줄 수 있고 그 함수를 Sigmoid 함수라고 한다.
결과적으로 우리는 다음과 같은 함수를 가설을 얻을 수 있다.

가설을 세웠다면 이제 무엇을 해야겠는가? 바로, Cost 함수를 Minimize 하는 것이다.
그런데 이전까지의 Linear 한 가설의 Cost function과는 조금 다른 모양이 될 것임을 예측할 수 있다.
Linear 한 가설의 Cost function은 Wx(1차 방정식)의 제곱의 형태를 띠므로 2차 방정식 모양이 될 것이지만
Sigmoid를 제곱한다면 아래와 같은 모양을 띌 것이다.

그런데 위와 같은 함수 형태를 띠면 Gradient 알고리즘을 적용할 때 시작점에 따라 결과가 다르게 나올 수 있다. (기울기가 0이 되는 부분이 여러 군데 존재하기 때문에 Global Minimum이 아닌 Local Minimum에 도달할 수 있다.)
따라서 위와 같은 Cost function은 사용할 수 없고 새로운 가설이 세워졌으니 새로운 Cost function을 세워야 한다.

y = 1 일 때,
H(x) = 1 -> cost(1) = -log(1) = 0
H(x) = 0 -> cost(0) = -log(0) = 무한대
y = 0 일 때,
H(x) = 0 -> cost(0) = -log(1-0) = 0
H(x) = 1 -> cost(1) = -log(1-1) = 무한대
예측이 성공한다면 cost 값이 0이 될 것이며 예측에 실패한다면 무한대가 되는 것을 기반으로 Cost function을 위와 같이 구성한다. ( 두 개의 Cost function 그래프를 이어 붙이면 실제로 이전의 밥그릇 모양의 함수 형태가 된다. )

위와 같은 Cost function을 사용할 때 y = 1 인 부분과 y = 0 인 부분을 if 조건문을 통해 나눠야 하는 불편함이 있어서 두 개의 식을 하나로 합쳐서 사용한다.

y = 1 일 때는 1-y = 0 이 되어서 c = -log(1+(x))가 되며 y = 0 일 때는 -log(1-H(x))가 되어서 앞서서 봤던 케이스가 나뉜 Cost function과 같아질 것이다.
그 후, Minimize 하기 위하여 Gradient 알고리즘을 사용하기 위해 Cost function을 미분을 해야 한다.

실제 코드를 짤 때는 위와 같이 TensorFlow에서 제공하는 함수를 사용하면 된다.
이제 실제 소스 코드에는 어떤식으로 Logistic classification을 구현하는지 확인해 보자.
강의 상의 코드가 올바르게 작동하지 않기에 다른 코드를 가져와서 돌려보았다..
import tensorflow as tf
import numpy as np
x_train = np.array([
[1, 2],
[2, 3],
[3, 1],
[4, 3],
[5, 3],
[6, 2]], dtype=np.float32)
y_train = np.array([
[0],
[0],
[0],
[1],
[1],
[1]], dtype=np.float32)
x_test = np.array([[5, 2]], dtype=np.float32)
y_test = np.array([[1]], dtype=np.float32)
# tf.data.Dataset 파이프라인을 이용하여 값을 입력
# from_tensor_slices 클래스 매서드를 사용하면 리스트, 넘파이, 텐서플로 자료형에서 데이터셋을 만들 수 있음
dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(len(x_train))
W = tf.Variable(tf.zeros([2, 1]), name='weight')
b = tf.Variable(tf.zeros([1]), name='bias')
# 원소의 자료구조 반환
# dataset.element_spec
# Logistic regression (sigmoid function 사용) features = X
def logistic_regression(features):
hypothesis = tf.sigmoid(tf.matmul(features, W) + b)
return hypothesis
# cost function 구현
def loss_fn(features, labels):
hypothesis = logistic_regression(features)
cost = -tf.reduce_mean(labels * tf.math.log(hypothesis) + (1 - labels) * tf.math.log(1 - hypothesis))
return cost
# Gradient descent 알고리즘 구현을 위한 기울기 반환 (미분)
def grad(features, labels):
with tf.GradientTape() as tape:
loss_value = loss_fn(features, labels)
return tape.gradient(loss_value, [W, b])
# 경사 하강법 사용
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
# 횟수 3000번
EPOCHS = 3000
# X와 Y 데이터를 features 와 labels로 나누는 형식으로 구현
for step in range(EPOCHS + 1):
for features, labels in iter(dataset):
hypothesis = logistic_regression(features)
grads = grad(features, labels)
optimizer.apply_gradients(grads_and_vars=zip(grads, [W, b]))
if step % 300 == 0:
print("Iter: {}, Loss: {:.4f}".format(step, loss_fn(features, labels)))
# print(hypothesis)
# 정확도 출력을 위한 함수
def accuracy_fn(hypothesis, labels):
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, labels), dtype=tf.int32))
return accuracy
test_acc = accuracy_fn(logistic_regression(x_test), y_test)
print('Accuracy: {}%'.format(test_acc * 100))
hypothesis 변수를 만들때 matmul을 이용하여 XW를 구현하고 TensorFlow에서 제공하는 sigmoid 함수를 이용하여 이전에 우리가 세웠던 가설에 맞게 구현해준다.
cost도 마찬가지로 두개의 경우를 하나로 합친 수식을 log 함수를 사용하여 구현한다.
또한, cast 함수를 통해 0.5를 초과하는 hypothesis의 output은 1, 이하는 0으로 반환시켜주며 그 반환한 값을 이용하여 accuracy 변수에 우리가 학습시킨 결과가 실제 Y와 같은지 equal 함수와 cast 함수를 통하여 전체의 평균을 내준다.
(전체 중에 결과가 맞는 데이터가 몇% 인지 확인하기 위하여)
스탭이 진행됨에 따른 cost의 변화를 출력하고 모든 학습이 종료되었을 때 Cast 하기 전의 Hypothesis 값과 Cast 하고 난 뒤인 Predicted 값(0, 1) 그리고 결과적으로 몇% 의 정답이 맞았는지 Accuracy 값을 출력하여준다.
결과
결과를 확인해 보면 cost 값이 학습이 진행됨에 따라 점점 줄어들어 0에 수렴해 간다는 것을 확인할 수 있으며 Hypothesis 값을 통해 테스트 데이터 셋을 통한 output을 확인할 수 있으며 그 output을 cast 함수를 통해 0과 1로 나누어 주어 결과적으로 test 데이터의 모든 결과가 맞아떨어져서 Accuracy 값이 1(100%)이 됨을 확인할 수 있다.

| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
|---|---|
| 8. Softmax classification (0) | 2020.04.22 |
| 6. Loading Data from File (0) | 2020.04.18 |
| 5. Multi-variable linear regression (0) | 2020.04.17 |
| 4. Hypothesis and Cost (0) | 2020.04.16 |