이번에는 Neural Network를 통해 학습에 문제였던 XOR 문제를 어떻게 푸는지 확인해보자.
초기의 단층의 시스템으로는 XOR 문제를 풀 수 없다는 것이 수학적으로 증명이 되었고 이후 여러층을 가진 시스템을 구성하면서 해결책을 제시했고 그 과정에서 각 층의 W, b를 구하는 것이 다시 문제가 되었다.
그렇다면 3개의 Logistic Regression을 통해(Neural Net) 어떤 식으로 XOR 문제를 해결하였는지 확인해보자.

위의 그림은 XOR 문제를 해결하는 하나의 예시이다. 위와 같이 하나의 시스템이 아닌 여러개의 시스템을 이용하여 우리가 원하는 XOR 문제의 결과를 도출해낼 수 있다.
x1 = 0, x2 =0 일때, XOR을 수행하면 0이 나와야 하는데 그 과정을 예로 들어 보겠다.


sigmoid 함수를 사용하면 위와 같은 결과가 나올 것이다. 여기서 y1, y2를 구하는 시스템에서 sigmoid 함수를 사용하지 않아도 결과는 같게 나온다.
위의 결과는 임의의 W, b 값을 주어준 상태로 결과 값을 도출해낸 것으로 XOR의 계산이 가능하다는 것을 보여준다.
결과적으로 아래와 같은 형태를 띨 것이다.

또한 x 데이터를 받는 두 개의 Logistic Regression은 아래와 같이 Vector 단위로 하나로 묶일 수 있다.

그렇다면 TensorFlow를 활용한 코드로 NN을 이해해보자.
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
# 랜덤시드
tf.compat.v1.set_random_seed(777)
# 데이터 셋
x_data = [[0, 0],
[0, 1],
[1, 0],
[1, 1]]
y_data = [[0],
[1],
[1],
[0]]
# 데이터 셋 구성
dataset = tf.data.Dataset.from_tensor_slices((x_data, y_data)).batch(len(x_data))
# 데이터 전처리
def preprocess_data(features, labels):
features = tf.cast(features, tf.float32)
labels = tf.cast(labels, tf.float32)
return features, labels
# weight, bias 선언 3개의 시스템
W1 = tf.Variable(tf.random.normal([2, 1]), name="weight1")
b1 = tf.Variable(tf.random.normal([1]), name="bias1")
W2 = tf.Variable(tf.random.normal([2, 1]), name="weight2")
b2 = tf.Variable(tf.random.normal([1]), name="bias2")
W3 = tf.Variable(tf.random.normal([2, 1]), name="weight3")
b3 = tf.Variable(tf.random.normal([1]), name="bias3")
# NN 구현 layer1, layer2 -> layer3
def neural_net(features):
layer1 = tf.sigmoid(tf.matmul(features, W1) + b1)
layer2 = tf.sigmoid(tf.matmul(features, W2) + b2)
# tf.concat 함수를 통해 데이터 횡방향 연결
layer3 = tf.concat([layer1, layer2], -1)
layer3 = tf.reshape(layer3, shape=[-1, 2])
hypothesis = tf.sigmoid(tf.matmul(layer3, W3) + b3)
return hypothesis
# cost 함수 구현
def loss_fn(hypothesis, labels):
cost = -tf.reduce_mean(labels * tf.math.log(hypothesis) + (1 - labels) * tf.math.log(1 - hypothesis))
return cost
# 정확도 측정 함수 구현
def accuracy_fn(hypothesis, labels):
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, labels), dtype=tf.float32))
return accuracy
# 학습 (cost minimize)
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
def grad(hypothesis, features, labels):
with tf.GradientTape() as tape:
loss_value = loss_fn(neural_net(features), labels)
return tape.gradient(loss_value, [W1, W2, W3, b1, b2, b3])
EPOCHS = 5000
for step in range(EPOCHS):
for features, labels in iter(dataset):
features, labels = preprocess_data(features, labels)
grads = grad(neural_net(features), features, labels)
optimizer.apply_gradients(grads_and_vars=zip(grads, [W1, W2, W3, b1, b2, b3]))
if step % 500 == 0:
print("Iter: {}, Loss: {:.4f}".format(step, loss_fn(neural_net(features), labels)))
x_data, y_data = preprocess_data(x_data, y_data)
test_acc = accuracy_fn(neural_net(x_data), y_data)
print("Testset Accuracy: {:4f}".format(test_acc))
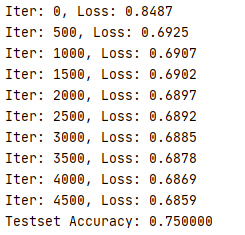
결과
'Machine Learning & Deep Learning' 카테고리의 다른 글
| 13. Relu (0) | 2020.04.30 |
|---|---|
| 11. Deep Neural Nets (0) | 2020.04.28 |
| 10. Training/Testing data set (0) | 2020.04.24 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |