Sigmoid 함수의 문제점
우선, Sigmoid 함수의 문제점을 말하기 위해 기존의 NN이 어떤식으로 동작하는지 복습해보자.

Input 데이터가 NN을 거쳐서 Output이 도출되고 그 Output과 실제 데이터의 차이를 loss(cost)라고 하며 이 loss의 미분을 통하여 Backpropagation 하여 NN을 학습시킨다.
그렇다면 loss의 미분은 기울기라고 할 수 있는데 sigmoid 함수의 특징상 양쪽으로 갈수록 기울기가 0에 가까워지며 그런 값들이 계속해서 곱해지면 결국 gradient가 소실되는 상황이 발생하고 Backpropagation 단계에서 이전 층이 전달받을 gradient가 없게 되는 현상이 생기는데 그것을 Vanishing Gradient라고 하고 이 현상이 sigmoid 함수의 문제점이라 할 수 있다. ( 양 극단의 미분값이 0이 되는 문제 )
Relu
위와 같은 문제를 해결할 수 있는 방법중 하나는 Relu 함수를 쓰는 것이다.
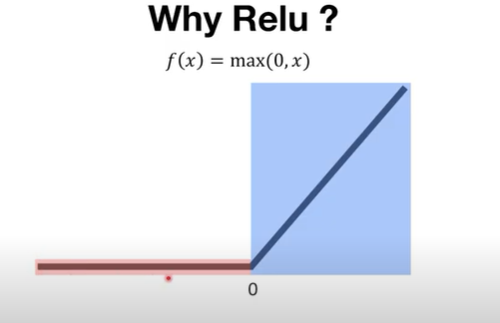
Relu 함수는 위와 같은 형태를 띠는데 0 이상일때 y=x 즉, gradient가 1이 되므로 네트워크의 층이 많아도 문제가 발생하지 않는다. 다만, 0 이하일때 즉, 음수일때는 기울기가 0이 되므로 문제가 발생한다. 그럼에도 효율적이고 간단해서 많이 사용된다.
'Machine Learning & Deep Learning' 카테고리의 다른 글
| 12. Neural Nets(NN) for XOR (0) | 2020.04.28 |
|---|---|
| 11. Deep Neural Nets (0) | 2020.04.28 |
| 10. Training/Testing data set (0) | 2020.04.24 |
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 8. Softmax classification (0) | 2020.04.22 |