# softmax 부분의 강의는 tensorflow 1.x 버전을 기준으로 작성하였습니다.
Softmax classification : Multinomial classification
이제는 Pass와 Fail의 두 가지 output을 가지는 것이 아니라 3가지 이상의 output을 가진 Multinomial classification에 대하여 알아볼 것이다.
그렇다면 공부시간, 출석을 가지고 성적을 예측하는 Multinomial Classification을 가지고 이해해보자.

위의 A, B, C라는 output을 가지는 y를 Binomial classification의 방식을 이용하여 나누는 작업을 해보자.

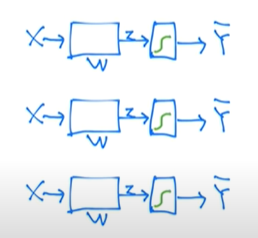
(C or Not), (B or Not), (A or Not)의 세 가지 Binomial classification 방식을 사용하여 Multinomial classification을 구현하였다.
오른쪽 사진은 Binomial 방식을 그림으로 표현한 것인데 설명하자면 input인 X 값이 weight(가중치)를 거쳐서 z가 되고 이 z가 sigmoid 함수를 거쳐서 Y-hat이 된다. Y-hat의 의미는 실제 output이 될 수 있는 1과 0인 Y에 반해 sigmoid를 거친 z의 값은 0~1 사이의 값을 가질 수 있고 그 값을 Y-hat이라고 표현한다.
결과적으로 이 Multinomial classification을 Matrix로 표현하면 아래와 같은 형태가 될 것이다.

그런데 이렇게 독립적으로 Matrix를 계산하는 것보다 하나의 Matrix로 합쳐서 계산하는 것이 효율적이기 때문에 Matrix를 합쳐주는 과정을 수행하여 준다.

이전의 방식은 Matrix의 곱을 수행하면 하나의 Scalar 값으로 반환되는데 합친 Matrix의 곱은 Vector 형식으로 반환됨을 볼 수 있다.

Binomial classification에서는 행렬 곱에 의해 반환된 값을 sigmoid 함수를 이용하여 0~1 사이의 값으로 변환시켜주었지만 Multinomial classification에서는 softmax 함수를 이용하여 0~1 사이로 변환시켜주며 합이 1이 되게 만든다.
(합이 1이라는 의미는 각각의 값이 확률이 된다는 의미이다. 위의 이미지에서 a는 0.7, b는 0.2, c는 0.1의 확률을 가지게 된다.)
그럼 우리의 output은 우리가 구한 확률이 아니라 특정 값이 되며 위의 예에서는 A or B or C가 되므로 이 확률을 가지고 A인지 B인지 C인지 구분해내는 과정이 필요한 것이다.

A, B, C를 구분해내기 위한 과정 중 확률이 가장 높은 것을 1로 만들어 주고 나머지를 0으로 만들어 주는 알고리즘을 ONE-HOT encoding이라고 하며 이 알고리즘을 통해 반환되는 1 또는 0을 통해 A, B, C를 결정지어준다.
(TensorFlow에서는 argmax라는 함수를 이용하여 이 알고리즘을 구현한다.)
그렇다면 이제 우리가 구한 S(y) 값과 실제 label인 Y 값을 통하여 cost function을 구하고 Minimize 하는 과정을 거쳐서 우리가 원하는 weight 값을 구하고 모델을 만들어야 한다. (우리가 예측한 값이 맞는지 틀린지에 대한


S(y)와 L 값(Y 값)의 차이를 구하기 위하여 CROSS-ENTOROPY라는 함수를 사용한다.
CROSS-ENTOROPY 함수를 사용하는 이유는 위의 이미지와 같이 우리가 예측한 S(y) 값과 실제 데이터 레이블인 L 값이 일치할 때는 0 일치하지 않을 때는 무한대로 결과가 나오기 때문에 일치할 때는 작은 값, 일치하지 않을 때는 큰 값이 나오는 cost function의 특성을 만족하기 때문이다.
S(y)와 cost function을 이용하여 측정하고자 하는 것은 맞추냐 못 맞추냐가 아니라 확률적으로 얼마나 정확히 맞추냐이므로 S(y) 값을 활용해야 하고(ONE-HOT encoding을 통해 반환되는 값이 아닌)
만약 0.7, 0.2, 0.1으로 예측한 위의 알고리즘과 0.8, 0.1, 0.1으로 예측한 새로운 알고리즘이 있다면 후자가 더 우월한 알고리즘이라는 것을 이러한 cost function으로 알아낼 수 있다.
결과적으로 아래와 같은 cost function을 결정할 수 있다.

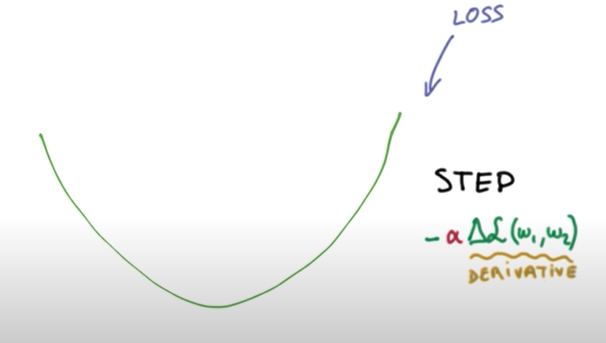
마지막으로 cost function을 minimize 해주어야 하는 W vector을 찾아주는 gradient descent 알고리즘을 사용하면 될 것이다. ( cost function의 미분을 통해 W 값을 update 하는 방식 )
실습
이제 실제로 TensorFlow를 이용하여 실습해보자.
TensorFlow에서는 softmax 함수를 제공하기 때문에 식으로 표현할 필요 없이 함수를 가져다 쓰면 된다.

softmax 과정을 거친 hypothesis을 가지고 cost function을 구현하고 minimize까지 완료하면 전체적인 모델 구성이 완료된다. (cross entropy 함수 형식을 사용)

코드
import tensorflow as tf
# x 데이터와 y 데이터 셋
x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5],
[1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]
# x 데이터셋의 크기는 n*4
# y 데이터셋의 크기는 n*3
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
# W의 크기는 [X data Column, Y data Column]
# b의 크기는 [Y data Column]
# 여기서 X는 입력 데이터 Y는 출력 데이터
# Variable은 TensorFlow가 자체적으로 변경시키는 것 (trainable)
# 랜덤한 값으로 주어 줌
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax를 이용하여 softmax 함수 사용
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy를 사용한 cost function 구현
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
a = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9],
[1, 3, 4, 3],
[1, 1, 0, 1]]})
print(a, sess.run(tf.arg_max(a, 1)))
결과
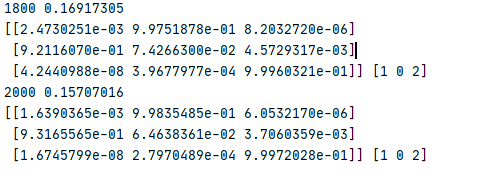
위의 소스코드를 구현함에 있어 복잡함을 줄이기 위해 TensorFlow에서 제공하는 함수를 이용해 보고 동물의 데이터를 통해 종을 분류하는 프로그램을 짜 보자.
import tensorflow as tf
import numpy as np
# Numpy의 loadtxt 함수를 이용하여 csv 파일 읽기
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
# x의 데이터 셋은 읽어온 파일의 전체행, 마지막 열(y) 데이터 제외
x_data = xy[:, 0:-1]
# y의 데이터 셋은 읽어온 파일의 전체행, 마지막 열(y)만
y_data = xy[:, [-1]]
# 클래스 개수 ( y가 0 ~ 6의 값을 가지므로 )
nb_classes = 7
# X, Y를 placeholder로 만들어 실행 단계에서 값을 넣어 줄 수 있도록 구현
# x(input)의 개수는 16, y(output)의 개수는 1 (0~6의 클래스 개수를 가진 1개의 y)
X = tf.placeholder(tf.float32, [None, 16])
Y = tf.placeholder(tf.int32, [None, 1])
# Y는 one-hot이 아닌 데이터이기 때문에 one-hot으로 바꿔주어야 한다.
Y_one_hot = tf.one_hot(Y, nb_classes)
# one_hot 함수를 이용하면 차원이 1차원 더해지기 때문에 reshape 함수를 통해 차원을 다시 맞춰주어야한다.
# [None, 7] 형태로 변환
Y_one_hot = tf.reshape(Y_one_hot, [-1, nb_classes])
# W, b 의 값을 변동가능한 Variable로 만들어 주고 16개의 input 종류를 가지고 one-hot을 거친 7개의 output
W = tf.Variable(tf.random_normal([16, nb_classes]), name = 'weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# 우리가 원하는 식을 세우고 softmax 함수를 통해 가설이 만듦
logits = tf.matmul(X, W) + b
hypothesis = tf.nn.softmax(logits)
# Cross entropy를 통한 cost function 구현
# 식을 직접 구현하는 것이 아닌
# softmax_cross_entropy_with_logits 함수를 이용하여 cross entropy 구현
cost_i = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# 예측한 값의 정확도를 확인하기 위해 accuracy 구현
prediction = tf.argmax(hypothesis, 1)
correct_prediction = tf.equal(prediction, tf. argmax(Y_one_hot, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2000):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 100 == 0:
loss, acc = sess.run([cost, accuracy], feed_dict={X: x_data, Y: y_data})
print("Step: {:5}\tLoss: {:.3f}\tAcc: {:.2%}".format(step, loss, acc))
pred = sess.run(prediction, feed_dict={X: x_data})
# flatten()은 y_data를 [[1], [0], ..] -> [1, 0, ..] 형태로 변경
# zip은 각각의 list를 p, y로 던져주기 편하게 하나로 묶음
for p, y in zip(pred, y_data.flatten()):
print("[{}] Prediction: {} True Y: {}".format(p == int(y), p, int(y)))
결과

'Machine Learning & Deep Learning' 카테고리의 다른 글
| 10. Training/Testing data set (0) | 2020.04.24 |
|---|---|
| 9. Learning rate, Data preprocessing, overfitting (0) | 2020.04.23 |
| 7. Logistic Regression (0) | 2020.04.20 |
| 6. Loading Data from File (0) | 2020.04.18 |
| 5. Multi-variable linear regression (0) | 2020.04.17 |